Kartais reikia parinkti vieną iš kelių veiksmų. Pasirinkimas vyksta, atsižvelgiant į sąlygas. Tikrinti reikia viena sąlyga mažiau negu yra galimų pasirinkimų:
Pvz.
if sąlyga1
then if sąlyga2
then sakinys1
else if sąlyga3
then sakinys2
else sakinys3
else if sąlyga4
then sakinys4
else sakinys5
Atliekamas tik vienas iš penkių sakinių, o kuris iš jų – priklauso nuo to kuri iš sąlygų teisinga.
Pvz. 9.1
Duota natūraliųjų skaičių seka. Sekos pabaigos požymis 0. Parašykime programą, kuri rastų sekos narių mažesnių už 10 sandaugą, dviženklių sekos narių kvadratų sumą, triženklių sekos narių sumą, suskaičiuotų sekos narius didesnius už 999.
var n, san, s10, s100, k : longint;
begin
read(n);
san := 1; S10 := 0; S100 := 0; k := 0;
while n <> 0 do
begin
if n < 10
then san := san * n
else if n < 100
then s10 := s10 + n * n
else if n < 1000
then s100 := s100 + n
else k := k + 1;
read(n)
end;
writeln('san = ', san, ', s10 = ', s10, ', s100 = ', s100, ', k = ', k)
end.
Labai dažnai sprendžiant praktinius uždavinius naudojami realūs skaičiai. Programavimo kalbose kintamieji įgyjantys tokias reikšmes yra aprašomi realiųjų skaičių tipu real.
Į ekraną išvedant realius skaičius (dažniausiai programos rezultatus) patartina nurodyti jų tikslumą.
Pvz. writeln(‘x = ‘, x : 5 : 3)
Antrasis skaičius nurodo kiek spausdinti po kablelio skaitmenų (skaičiaus tikslumą). Pirmasis skaičius nurodo kiek vietos iš viso skiriama kintamojo reikšmei išvesti į ekraną. Jeigu nurodoma per mažai vietos, programa pati pasiima tiek kiek trūksta, kad skaičius sutilptų.
Kvadratinės šaknies traukimas Pascal programavimo kalboje žymimas sqrt. Pvz. sqrt(x)
Pvz. 9.2Parašykime programą, kuri išspręstų kvadratinę lygtį. Lygties šaknys gali būti ne tik sveiki skaičiai, bet ir realūs. Žinome, kad sprendžiant kvadratinę lygtį reikia apskaičiuoti diskriminantą D. Jeigu jo reikšmė neigiama, tai lygtis šaknų neturi, jei D = 0, tai lygtis turi vieną šaknį, jei D teigiamas, tai lygtis turi dvi šaknis.
var a, b, c, d, x, x1, x2 : real;
begin
writeln('Įveskite lygties koeficientus');
read(a, b, c);
d := b * b – 4 * a * c;
if d < 0
then writeln('Lygtis šaknų neturi')
else if d = 0
then begin
x := -b /(2 * a);
writeln('Lygtis turi vieną šaknį x = ', x : 6 : 2)
end
else begin
X1 := (-b - sqrt(d)) / (2 * a);
X2 := (-b + sqrt(d)) / (2 * a);
writeln('x1 = ', x1 : 6 : 2, ', x2 = ', x2 : 6 : 2)
end
end.
1 tikrinamasis darbas
Pvz. 9.3
Parašykime programą, kuri išspręstų duotą lygčių sistemą su dviem nežinomaisiais.
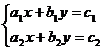
Kad parašyti programą, reikia mokėti spręsti tokią lygčių sistemą. Išnagrinėsime
vieną iš sprendimo būdų. Jį naudojant yra skaičiuojami dydžiai vadinami
determinantais.
D = a1b2 - a2b1 , Dx = c1b2 - c2b1 , Dy = a1c2 - a2c1
1) Jei D = 0 ir bent vienas iš skaičių Dx ir Dy nelygus nuliui, tai lygčių sistema neturi sprendinių.
2) Jei D = Dx = Dy = 0, tai lygčių sistema turi be galo daug sprendinių.
3) Jei D nelygu nuliui, tai lygčių sistema turi vieną sprendinį, skaičių porą
![]() ir
ir
![]() .
.
var a1, b1, c1, a2, b2, c2 : integer;
d, dx, dy : integer;
x, y : real;
begin
writeln('Įveskite pirmos lygties koeficientus');
read(a1, b1, c1);
writeln('Įveskite antros lygties koeficientus');
read(a2, b2, c2);
d := a1 * b2 – a2 * b1;
dx := c1 * b2 – c2 * b1;
dy := a1 * c2 – a2 * c1;
if (d = 0) and ((dx <> 0) or (dy <> 0))
then writeln('Lygčių sistema neturi sprendinių')
else if d <> 0
then begin
x := dx/d; y := dy/d;
writeln('x = ', x : 5 : 2, ', y = ', y : 5 : 2)
end
else writeln('Lygčių sistema turi be galo daug sprendinių')
end.
Pvz. Kompiuteris šiuos sakinius atliks nebūtinai taip kaip išdėstyta, todėl tokias konstrukcijas reikia naudoti atsargiai.
then if sąlyga2
then if sąlyga3
then sakinys2
else if sąlyga4
then sakinys3
else sakinys4
Užduotys
Nr.1
a) Duota skaičių seka, jos pabaigos požymis nulis. Parašykime
programą, kuri rastų sekos narių mažesnių už 100 kvadratų sumą, triženklių
sekos narių sumą, suskaičiuotų kiek sekos narių didesnių už 999 yra lyginiai.
b) Duota skaičių seka, jos pabaigos požymis nulis. Parašykime programą, kuri rastų vienženklių sekos narių sandaugą, mažesnių už 100 lyginių sekos narių kvadratų sumą, triženklių sekos narių, kurie baigiasi nuliu sumą, suskaičiuotų kiek sekos narių didesnių už 999 dalijsi iš 5.
Nr. 2Duota natūraliųjų skaičių seka. Sekos pabaigos požymis nulis. Parašykite programą, kuri rastų kiek sekoje yra skaičių, lygių duotam skaičiui a, kiek didesnių ir kiek mažesnių už jį.
Nr. 3
Parašykite programą, kuri spręstų lygtį ax = b, kur a ir b sveiki skaičiai.